| Задать ориентацию объекта в пространстве можно достаточно большим количеством способов. Первое, что приходит на ум - это конечно, задание углов по трём осям - углы Эйлера, они же рысканье, тангаж и крен. В панде задаётся процедурой setHpr() - сокращение от английских названий Heading, Pitch, Roll. Однако, в некоторых случаях, такое задание углов может вызвать ощутимую пачку неудобств, например, если требуется повернуть объект от одного угла до другого. Казалось бы чего проще, а нет, он вдруг начинает вертеться совсем не туда куда нам нужно или вместо короткой дуги выбирает длинную, так что приходится добавлять кучу проверок и условий. Вот здесь нам и стоит вспомнить страшное слово кватернион. Кватернион - способ задать ориентацию с помощью вектора направления и поворота вокруг этого вектора. 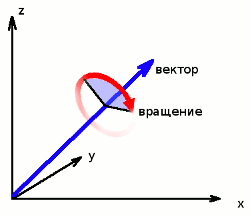 alpha - угол поворота
V - вектор направления
q - кватернион
q = [cos(alpha/2), V*sin(alpha/2)] Теперь о полезных свойствах:
Умнжив кватернионы - q1*q2 - мы получим такое результирующее вращение, как если бы объект сначала повернули на q1 а потом на q2, при этом q1*q2 не равно q2*q1. От положения множителей зависит какой поворот выполняется сначала.
Сложив кватернионы q1 + q2 мы получим вращение, находящееся между этими двумя кватернионами (смесь вращений). Если оба кватерниона нормализованы, то результирующее вращение будет точно посередине.
Умножение кватерниона на число, не равное 0 не изменит вращения, но может быть полезно в комбинации со сложением. Пример вышенаписанного в панде. Для наглядности вбивалось напрямую в интерпретаторе питона. Показано сложение, умножение и интерпояция по кратчайшей дуге с помощью сложения и умножения на число:
Code
>>> from pandac.PandaModules import *
>>> q1, q2 = Quat(), Quat()
>>> q1.setHpr((15,0,0))
>>> q2.setHpr((30,0,0))
>>> q3 = q1 + q2
>>> q3.getHpr()
VBase3(22.5, 0, 0)
>>> q3 = q1 * q2
>>> q3.getHpr()
VBase3(45, 0, 0)
>>> for i in xrange(10):
... q3 = q1*((i+1)*0.1)+q2*(1-(i+1)*0.1)
... print q3.getHpr()
...
VBase3(28.5031, 0, 0)
VBase3(27.0041, 0, 0)
VBase3(25.5036, 0, 0)
VBase3(24.0021, 0, 0)
VBase3(22.5, 0, 0)
VBase3(20.9979, 0, 0)
VBase3(19.4964, 0, 0)
VBase3(17.9959, 0, 0)
VBase3(16.4969, 0, 0)
VBase3(15, 0, 0)
>>>
Более подробно о кватернионах пишут умные дядьки здесь http://www.gamedev.ru/code/articles/?id=4215
|